Train- and val losses drop then oscillates - help appreciated

General Discussion
#1

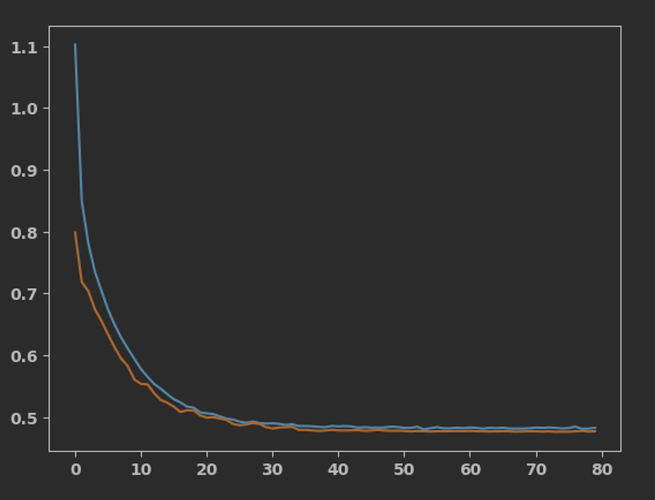
Hey guys!

Like the title says, I would love some help on this quite general problem for me. Too often while building models (mostly Keras), I end up in a situation where I manage to get both training- and val loss down to about 0.5 (this time for a rather simple regression problem), but then it starts to oscillates and I am unsure of how to proceed.

I am using this Kaggle dataset: Housing Price Prediction Data | Kaggle

What I’ve tried to far:

Many different network architecture (started out simple and made it gradually deeper/wider), but of course, I might have missed a sweet spot.

Added Dropout, L2-reg and switched from Relu to Leaky Relu

Fiddled around with the learning rate quite a bit - now using both a ReduceLROnPlateau and a scheduler.

Tried different batch sizes (between 32 and 256).

Tried SGD instead of Adam, then switched back.

Tried changing the number of epochs (ranging from 50 to 200).

Code:

Early stopping

early_stopping_callback = EarlyStopping(monitor=‘val_loss’, patience=35, verbose=1, restore_best_weights=True)

Reduce learning rate on loss plateau

reduce_lr = ReduceLROnPlateau(monitor=‘val_loss’, factor=0.1, patience=15, min_lr=0.0001, verbose=1)

opt = Adam(learning_rate=0.0001)

Add the learning rate scheduler to the callbacks

scheduler_callback = LearningRateScheduler(lambda epoch: 0.001 * np.exp(-epoch / 10.))

Batch size

batch_size = 128

Regularization factor

l2_reg = 0.001

%% Set up model

model = Sequential([
Dense(16, kernel_regularizer=l2(l2_reg), input_shape=(X_train_scaled.shape[1],)),
BatchNormalization(),
LeakyReLU(alpha=0.01),
Dropout(0.1),

Dense(48, kernel_regularizer=l2(l2_reg)),
BatchNormalization(),
LeakyReLU(alpha=0.01),
Dropout(0.15),

Dense(80, kernel_regularizer=l2(l2_reg)),
BatchNormalization(),
LeakyReLU(alpha=0.01),
Dropout(0.2),

Dense(80, kernel_regularizer=l2(l2_reg)),
BatchNormalization(),
LeakyReLU(alpha=0.01),
Dropout(0.2),

Dense(80, kernel_regularizer=l2(l2_reg)),
BatchNormalization(),
LeakyReLU(alpha=0.01),
Dropout(0.15),

Dense(64, kernel_regularizer=l2(l2_reg)),
BatchNormalization(),
LeakyReLU(alpha=0.01),
Dropout(0.15),

Dense(1, activation='linear', kernel_regularizer=l2(l2_reg))

])

model.compile(optimizer=opt, loss=‘mean_squared_error’, metrics=[‘mean_absolute_error’])

%% Train model

history = model.fit(
X_train_scaled, y_train_scaled,
epochs=80,
batch_size=batch_size,
validation_data=(X_val_scaled, y_val_scaled),
shuffle=True,
callbacks=[checkpoint_callback, early_stopping_callback, scheduler_callback, reduce_lr]
)

Loss:

image
image1405×1072 75.9 KB

I would highly appreciate any tips or help to get around this problem. From what I understand it’s quite common. Many thanks in advance!

#3

@JN37

It looks like you’ve put in a lot of effort into optimizing your model for a regression problem on the Housing Price Prediction dataset. Here are a few suggestions that might help you further:

  1. Experiment with model complexity. You’ve tried different architectures, but it might be worth exploring simpler or more complex models. Sometimes a sweet spot is hard to find, and it’s okay to revisit simpler designs.
  2. Ensure that your input data is properly normalized. For regression tasks, it’s crucial to have input features on a similar scale. Batch normalization is helpful, but double-check the scaling of your original features.
  3. Continue experimenting with the learning rate. You’ve implemented a scheduler, which is good. However, try different initial learning rates or other schedules to see if they have an impact.
  4. Investigate if there are any specific features that might benefit from additional preprocessing or engineering. Sometimes transforming or combining features can enhance model performance.
  5. Consider ensemble methods. Building multiple models and combining their predictions can often lead to improved generalization.
  6. Examine the behavior of your model on the validation set. If both training and validation losses are oscillating, it could be a sign of overfitting. Adjust regularization or dropout rates accordingly.
  7. Review the learning rate scheduler’s impact. It might be worth trying different schedules or adjusting the parameters.
  8. Analyze the residuals (the differences between predicted and actual values). This might give insights into specific patterns that your model is struggling with.
  9. Try different loss functions. For regression tasks, mean squared error is common, but depending on your specific problem, other loss functions might be more suitable.
  10. Consider a more systematic hyperparameter search. Tools like grid search or random search can help explore a broader range of hyperparameters.
  11. Visualize the training dynamics. Plotting metrics over time can reveal when the oscillations start and if they correlate with specific events like learning rate changes or epochs.

Remember, it’s a bit of trial and error, and each dataset/model combination can behave differently

1 Like